I've been trying to find why wider tyres on cars yield more grip. Most explanations involve the assumption that wider tyres bring with them more road contact area however, the most common model used to describe a tyre is that of a balloon i.e. contact patch size is related to tyre air pressure and the load borne by the tyre. This means that no matter the size of the tyre, for a given air pressure and load, the contact patch will be constant. I was unable to find an explanation of why a wider tyre would increase the contact area so I decided to try to create my own.
It is quite possible that this model/explanation has been suggested before but I couldn't find it online anywhere so hopefully this will rectify that issue.
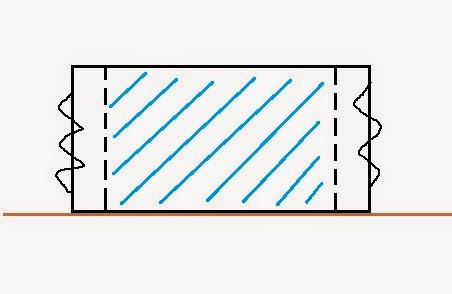
The crux of this explanation is the following model. To help explain the model I'll use this crude representation of a tyre cross section as viewed from the front.

In this model the air in the tyre is shown in blue, the tyre sidewalls are shown on either side of the air section as springs. To understand this model, the blue air section should be conceptualised as a third spring. Depending on the ratio of the stiffness of the sidewall springs to the air section springs, the air section will bear more or less of the weight. By increasing the width of the tyre the spring rate of the air section is effectively increased. This is caused by the rate of change of surface area to deflection being greater on a wider tyre.
Below is the formula I used to calculate the surface area required to support the load in terms of the included variables.
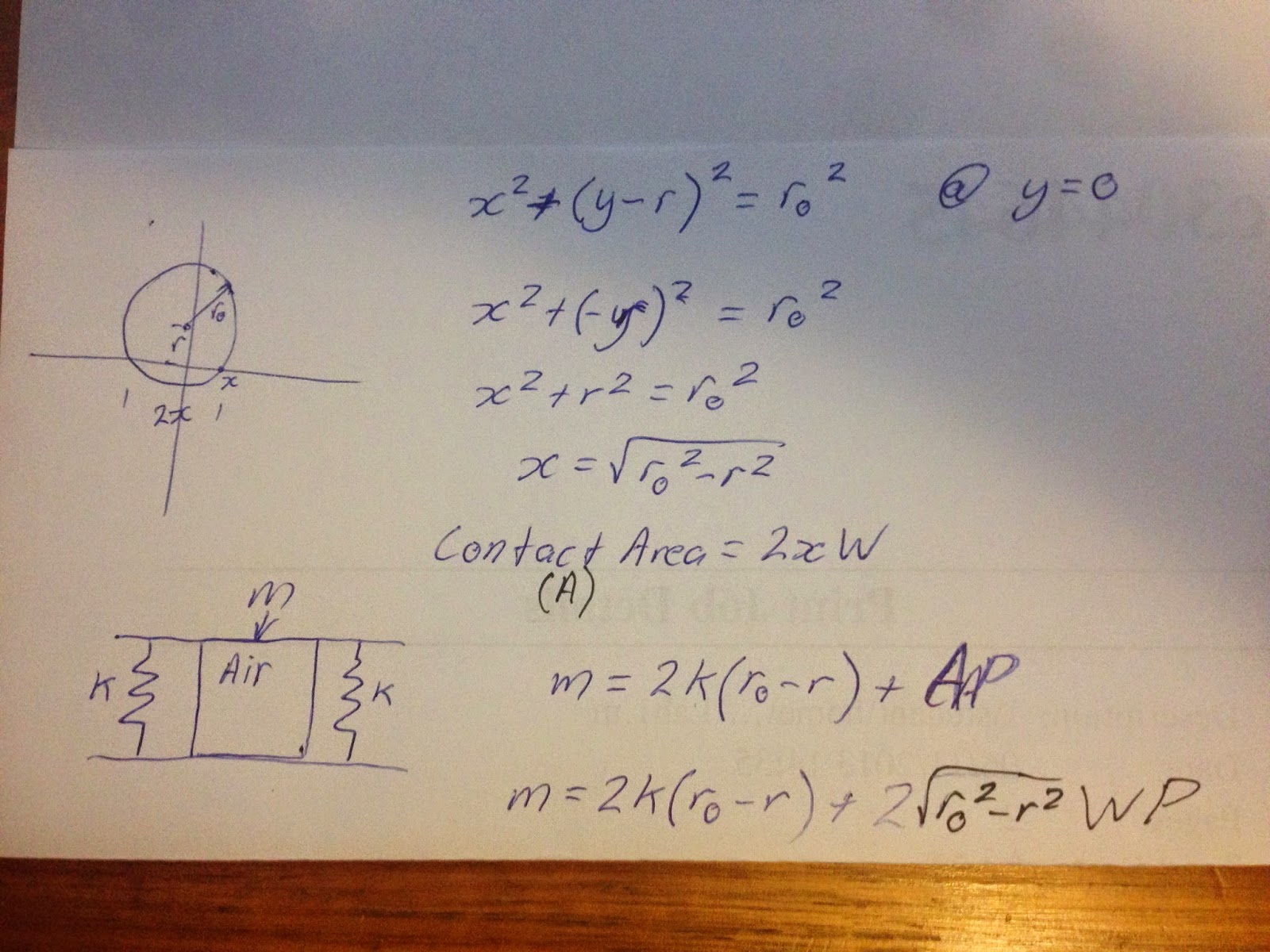
The first section is an approximation of the contact area of the tyre under load. The second section is the sum of forces from the three springs. The only unknown is r so by rearranging for this variable, and solving for various weights and two different width tyres, the surface area can be calculated and compared for the two tyres.
I used Matlab to generate data and plot the results. The script and results are included below.
width1 = 0.195; % Metres.
width2 = 0.215;
rimdia = 15; % Inches.
Press = 28; % PSI.
g = 9.81;
profile = 0.5;
r0 = 0.0254*rimdia/2+width1*profile; % Using same sidewall height for both tyres.
m = [1:600];
F = g.*m;
k = 70*g/0.005; % Person standing in rimless tyre.
P = Press*6894.8; % 28PSI.
r1 = (sqrt(4*r0^2*P^4*width1^4+4*r0*k*F*P^2*width1^2-F.^2*P^2*width1^2)+2*r0*k^2-k*F)/(2*(k^2+P^2*width1^2)); % Tyre 1.
r2 = (sqrt(4*r0^2*P^4*width2^4+4*r0*k*F*P^2*width2^2-F.^2*P^2*width2^2)+2*r0*k^2-k*F)/(2*(k^2+P^2*width2^2)); % Tyre 2.
A1 = 2*sqrt(r0^2-r1.^2)*width1*10^6;
A2 = 2*sqrt(r0^2-r2.^2)*width2*10^6;
Area_Difference = (A2(150)-A1(150)) % Area difference.
figure(1)
plot(m,A1,'b',m,A2,'r')
title('Contact Patch v Weight')
xlabel('Load (kg)')
ylabel('Area (mm^2)')
legend('Smaller','Larger','Location','SouthEast')
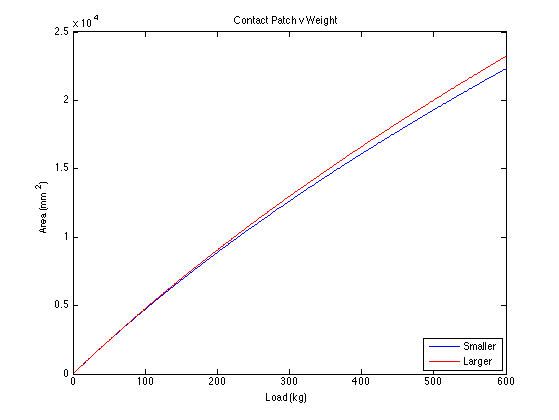
As can be seen the wider tyre has a larger contact area for a given load. A larger contact area doesn't, inherently, explain the extra grip however, explanations of why it can increase grip are available on the Internet. I've included below links to the best two explanations I've found.
Posts by 'Ciro' http://www.f1technical.net/forum/viewtopic.php?f=6&t=9333
First post on this page http://www.reddit.com/r/askscience/
I'll try to improve this explanation over time but hopefully some sense can be made of it as is.